Bentuk umum fungsi kuadrat adalah f(x) = ax2 + bx + c, dengan a ≠ 0
Sumbu simetri : x = -b/(2a)
Nilai maksimum y = -D/(4a), hanya berlaku jika a < 0
Nilai minimum y = -D/(4a), hanya berlaku jika a > 0
Koordinat titik puncak (-b/(2a), -D/(4a))
Menyusun fungsi kuadrat
1. Fungsi kuadrat yang melalui titik (a, 0) dan (b, 0) adalah
y = a(x - a)(x - b)
2. Fungsi kuadrat yang memiliki koordinat puncak (a, b) adalah
y - b = a(x - a)2
Sifat-sifat koefisien fungsi kuadrat :
a> 0 è parabola membuka ke atas
a < 0 è parabola membuka ke bawah
c > 0 è parabola memotong sumbu y positif
c < 0 è parabola memotong sumbu y negatif
c = 0 è parabola melalui (0, 0)
Diskriminan , D = b2 – 4ac
D > 0 parabola memotong sumbu x di dua titik
D = 0 parabola menyinggung sumbu x
D < 0 parabola tidak memotong sumbu x
Khasus fungsi kuadrat definit è D < 0
1. Definit positif , artinya nilai y selalu positif berapapun nilai x, atau parabola
seluruhnya berada di atas sumbu x. Ini terjadi jika
seluruhnya berada di atas sumbu x. Ini terjadi jika
a > 0
D <0
2. Definit negatif, artinya nilai y selalu positif berapapun nilai x, atau parabola
seluruhnya berada di bawah sumbu x. Ini terjadi jika
seluruhnya berada di bawah sumbu x. Ini terjadi jika
a < 0
D < 0
Hubungan antara parabola y = ax2 + bx + c dengan gris y = k
ax2 + bx + c = k
ax2 + bx + c-k = 0
maka D = b 2 – 4a(c - k)
1. D > 0 è parabola dan garis berpotongan di 2 titik
2. D = 0 è parabola dan garis saling bersinggungan
3. D < 0 è parabola dan garis tidak berpotongan
Hubungan antara parabola y = ax2 + bx + c dengan gris y = mx + n
ax2 + bx + c = mx + n
ax2 + (b-m)x + c-n = 0
maka D = (b – m)2 – 4a(c - n)
1. D > 0 è parabola dan garis berpotongan di 2 titik
2. D = 0 è parabola dan garis saling bersinggungan
3. D < 0 è parabola dan garis tidak berpotongan
Hubungan antara parabola y = ax2 + bx + c dan parabola y = px2 + qx + r
ax2 + bx + c = px2 + qx + r
(a - p) x2 + (b-q) x + c- r = 0
D = (b – q)2 – 4(a – p)(c – r)
1. D > 0 è kedua parabola berpotongan di 2 titik
2. D = 0 è kedua parabola saling bersinggungan
3. D < 0 è kedua parabola tidak berpotongan
Berikut ini adalah soal-soal fungsi kuadrat
1. Jika f(x) = x2 - 6x + 10 maka sumbu simetri dari f(x) adalah ...
Jawab :
Sumbu simetri
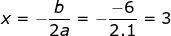
2. Fungsi f(x) = -x2 + 8x + 1 mengalami maksimum pada saat x = ...
Jawab :
Nilai maksimum terjadi pada sumbu simetri, jadi yang ditanyakan soal adalah sumbu simetrinya
maka
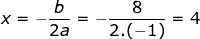
3. Nilai minimum dari fungsi f(x) = x2 - 4x + 8 adalah
Jawab :
Nilai minimum didapat dari
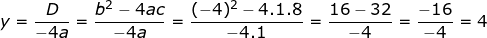
Cara II

hasil ini tinggal kita substitusikan ke f(x) sehingga
y = f(2) = 22 - 4.2 + 8 = 4 - 8 + 8 =4
4. Jika fungsi f(x) = -2x2 + 12x + 15 maka nilai maksimumnya adalah ....
Jawab :
Nilai maksimum adalah
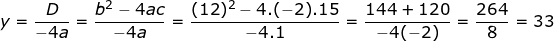
Cara II
kita cari nilai x nya dulu
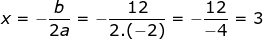
Nilai maksimunya adalah
y = f(-3) = -2.32 + 12.3 + 15 = -18 + 36 + 15 = 33
5. Fungsi f(x) = -3x2 + (p+2) x + 9 memiliki sumbu simetri x = 2. Nilai p sama dengan ...
Jawab :
sumbu simetri
x = 2
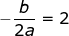
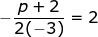
p + 2 = 12
p = 10
6. Agar fungsi f(x) = 2x2 - (k-1)x + 14 memiliki nilai minimum untuk x = 5 maka nilai k sama dengan ...
Jawab :
Nilai minimum terjadi pada sumbu simetri
x = 5
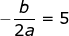
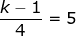
k - 1 = 20
k = 21
1. Jika f(x) = x2 - 6x + 10 maka sumbu simetri dari f(x) adalah ...
Jawab :
Sumbu simetri
2. Fungsi f(x) = -x2 + 8x + 1 mengalami maksimum pada saat x = ...
Jawab :
Nilai maksimum terjadi pada sumbu simetri, jadi yang ditanyakan soal adalah sumbu simetrinya
maka
3. Nilai minimum dari fungsi f(x) = x2 - 4x + 8 adalah
Jawab :
Nilai minimum didapat dari
Cara II
hasil ini tinggal kita substitusikan ke f(x) sehingga
y = f(2) = 22 - 4.2 + 8 = 4 - 8 + 8 =4
4. Jika fungsi f(x) = -2x2 + 12x + 15 maka nilai maksimumnya adalah ....
Jawab :
Nilai maksimum adalah
Cara II
kita cari nilai x nya dulu
Nilai maksimunya adalah
y = f(-3) = -2.32 + 12.3 + 15 = -18 + 36 + 15 = 33
5. Fungsi f(x) = -3x2 + (p+2) x + 9 memiliki sumbu simetri x = 2. Nilai p sama dengan ...
Jawab :
sumbu simetri
x = 2
p + 2 = 12
p = 10
6. Agar fungsi f(x) = 2x2 - (k-1)x + 14 memiliki nilai minimum untuk x = 5 maka nilai k sama dengan ...
Jawab :
Nilai minimum terjadi pada sumbu simetri
x = 5
k - 1 = 20
k = 21
jika mempunyai soal silagkan ditanyakan.. di komentar...
gan ketikannya ada yang rancu
ReplyDelete1. Definit positif , artinya nilai y selalu positif berapapun nilai x, atau parabola
seluruhnya berada di atas sumbu x. Ini terjadi jika
a > 0
D <0
2. Definit negatif, artinya nilai y selalu positif berapapun nilai x, atau parabola
seluruhnya berada di bawah sumbu x. Ini terjadi jika
a < 0
D < 0
kok positif semua ?
emang begitu ?
oh ya thank's gan atas infonya